Mathematics is everywhere, a small equation you studied in your childhood is been a big reason for many changes in engineering and technology around the world. In 2013, famous author Ian Stewart published a book “17 Equations That Changed The World“. This book elaborately explains each equation and how it moulded engineering to human accessible day to day technologies, which is really inspired me to write this. In this article, ilovephd summarise these 17 Equations and its applications.
1. Pythagoras’s Theorem
The Pythagorean Theorem is a statement in geometry that shows the relationship between the lengths of the sides of a right triangle – a triangle with one 90-degree angle.
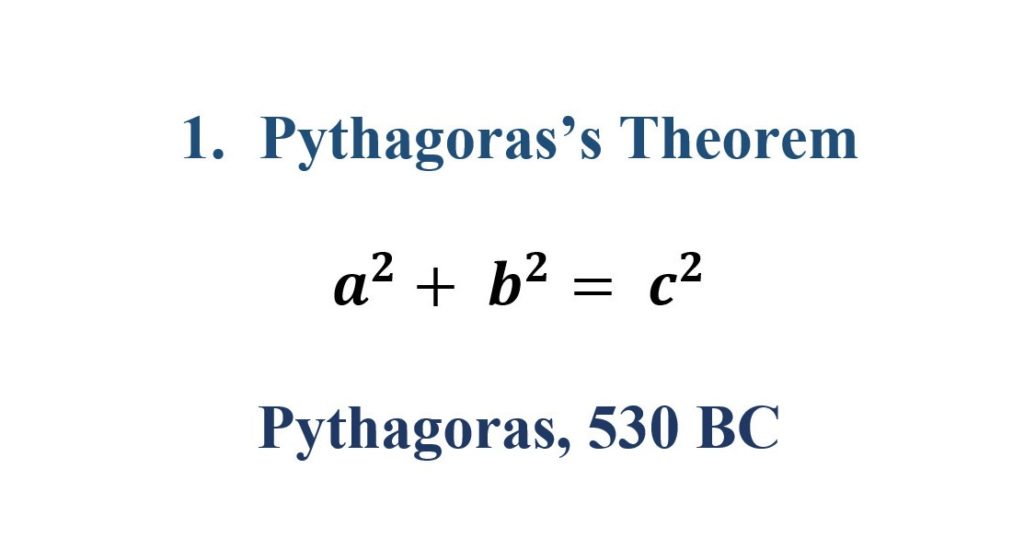
Applications of Pythagoras’s Theorem
The Pythagorean Theorem widely used in Architecture and Construction, Laying Out Square Angles, Surveying, and Navigation.
2. Logarithms
A logarithm is the power to which a number must be raised in order to get some other number .
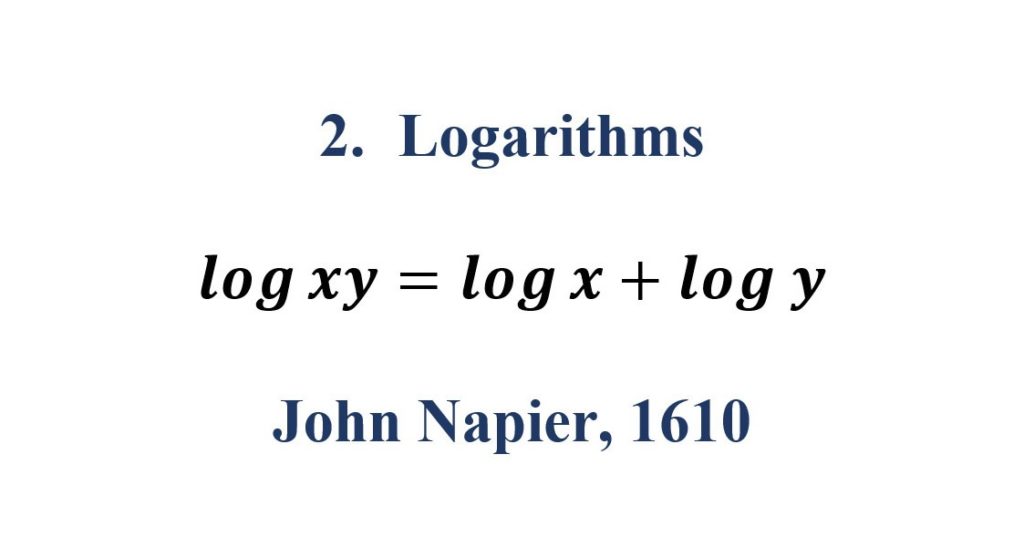
Applications of Logarithms
Logarithms widely used to measure Earthquake intensity measurement, Acid measurement of solutions(pH Value), Sound intensity measurements, and express larger value.
3. Calculus
Calculus is a form of mathematics which was developed from algebra and geometry. It is made up of two interconnected topics, differential calculus, and integral calculus.
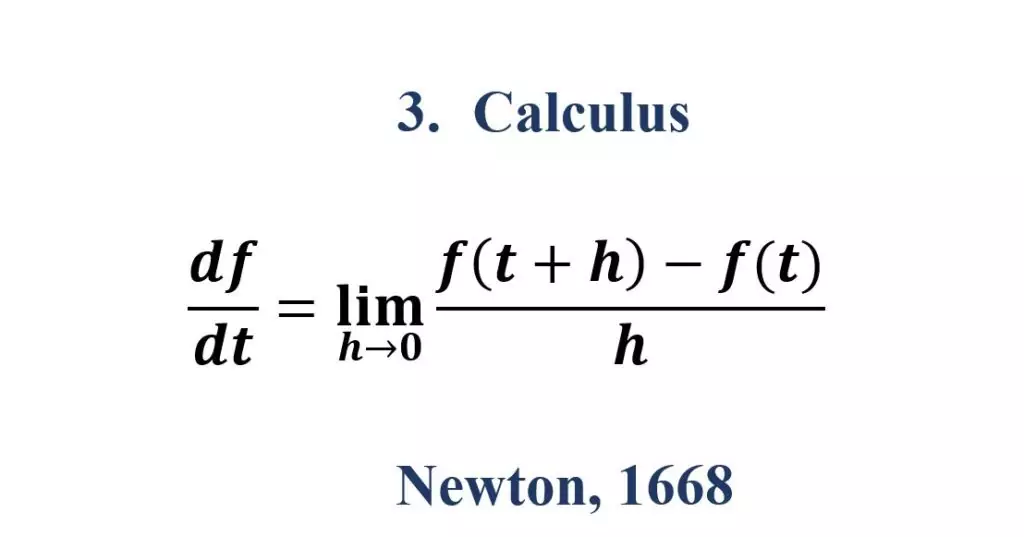
Applications of Calculus
Calculus is widely used for engineers, scientists, and economists. The contribution of these professionals has a huge impact on our daily life – from your microwaves, cell phones, TV, and car to medicine, economy, and national defense.
4. Law of Gravity
Every object in the Universe attracts every other object with a force directed along the line of centers for the two objects that is proportional to the product of their masses and inversely proportional to the square of the separation between the two objects.
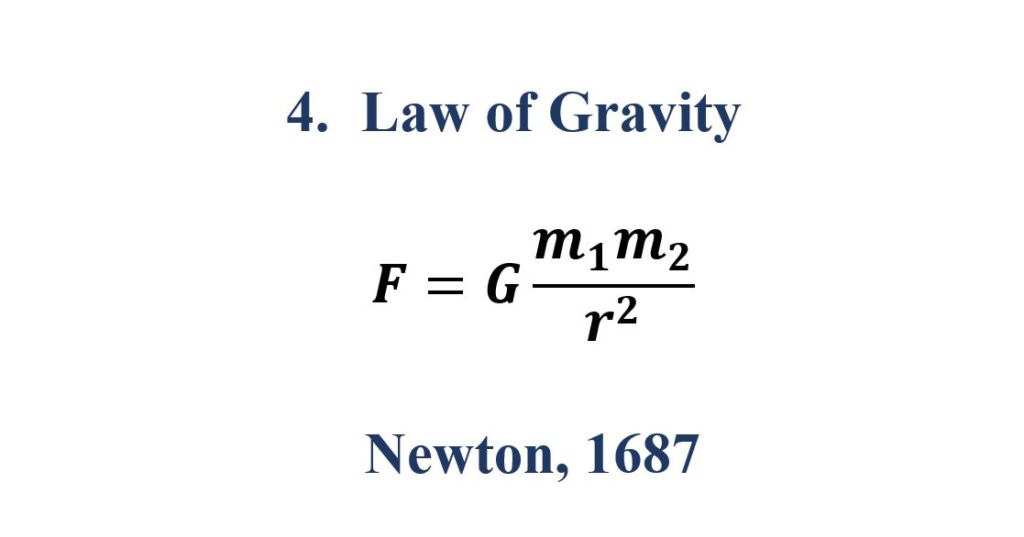
The significance of Gravitational Laws:
Gravitational laws are used in many ways from small bicycle manufacturing to the aerodynamics of a Rocket.
5. The Square Root of Minus One
Imaginary number is a complex number that can be written as a real number multiplied by the imaginary unit i, which is defined by its property i2 = −1.
The significance of the Imaginary number
When we get the square root of -1, we replace it with the shortcut i, which is called the “imaginary” number because negative square roots don’t actually exist (and it’s much easier to keep writing i than to write out the square root every time). That way, we keep the “imaginary” number just in case we will make the number useful again later in another equation by squaring it or multiplying it by a different imaginary number or something. And it turns out, in EE, this happens all the time.
6. Euler’s Formula for Polyhedra
A (convex) polyhedron is called a regular convex polyhedron if all its faces are congruent to a regular polygon, and all its vertices are surrounded alike. Plain experimentation with sticks will allow you to easily construct 5 regular polyhedra: tetrahedron, cube, octahedron, icosahedron, and dodecahedron.
7. Normal Distribution
The normal distribution, also known as the Gaussian distribution, is a probability distribution that is symmetric about the mean, showing that data near the mean are more frequent in occurrence than data far from the mean.
8. Wave Equation
The wave equation is an important second-order linear partial differential equation for the description of waves—as they occur in classical physics—such as mechanical waves (e.g. water waves, sound waves and seismic waves) or light waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics.
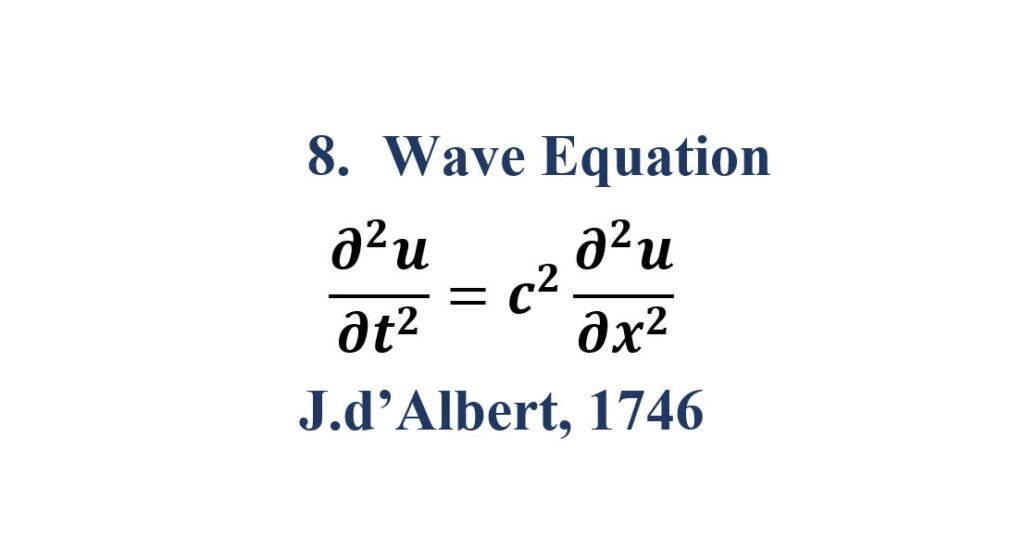
9. Fourier Transform
The Fourier transform (FT) decomposes a function of time (a signal) into the frequencies that make it up, in a way similar to how a musical chord can be expressed as the frequencies (or pitches) of its constituent notes.
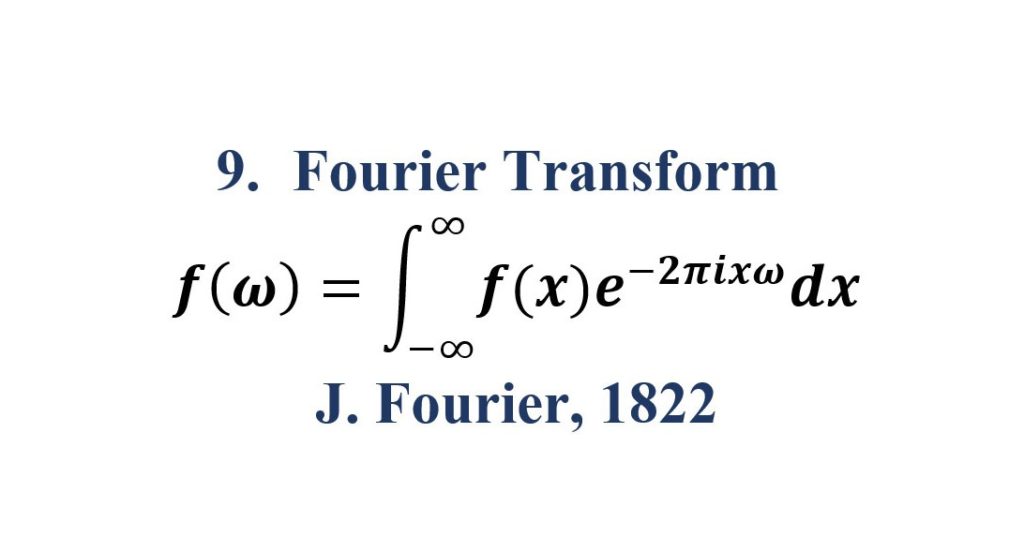
Applications of Fourier Transform:
- Designing and using antennas·
- Image Processing and filters
- Transformation, representation, and encoding
- Smoothing and sharpening
- Restoration, blur removal, and Wiener filter
- Data Processing and Analysis
- Seismic arrays and streamers
- Multibeam echo sounder and side scan sonar
- Interferometers — VLBI — GPS
- Synthetic Aperture Radar (SAR) and Interferometric SAR (InSAR)
- High-pass, low-pass, and band-pass filters
- Cross-correlation — transfer functions — Coherence
- Signal and noise estimation — encoding time series.
10. Navier – Stokes Equation
This equations arise from applying Isaac Newton’s second law to fluid motion, together with the assumption that the stress in the fluid is the sum of a diffusing viscousterm (proportional to the gradient of velocity) and a pressure term hence describing viscous flow.
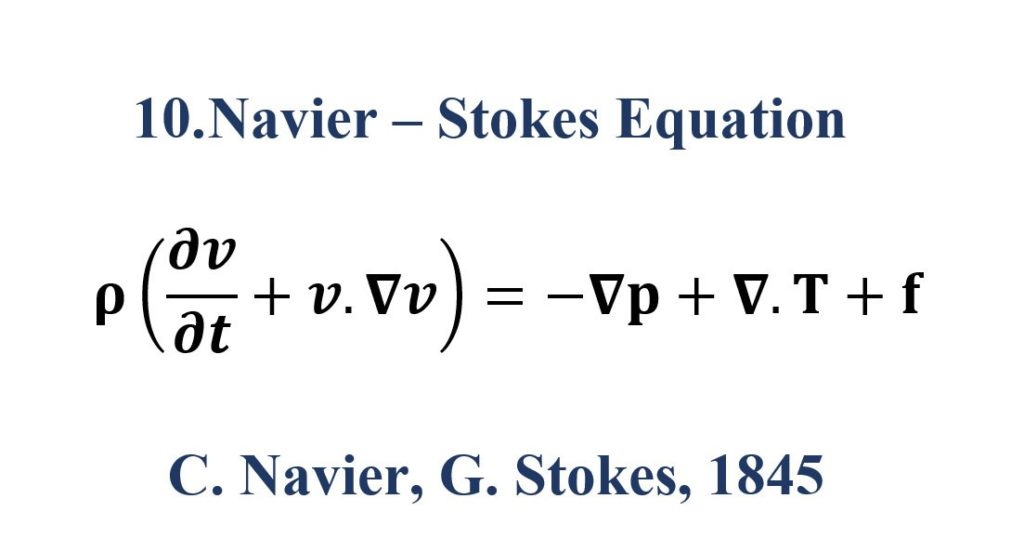
Navier Stokes equation is used to describe the flow characteristics of a Newtonian fluid. A fluid in which relation between stress and rate of strain is linear. In other words, a fluid obeys Newton law of viscosity. Honey, Benzene, Water, Kerosene oil, are just a few examples of a Newtonian fluid.
11. Maxwell’s Equations
Maxwell’s equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electromagnetism, classical optics, and electric circuits. The equations provide a mathematical model for electric, optical and radio technologies, such as power generation, electric motors, wireless communication, lenses, radar etc.
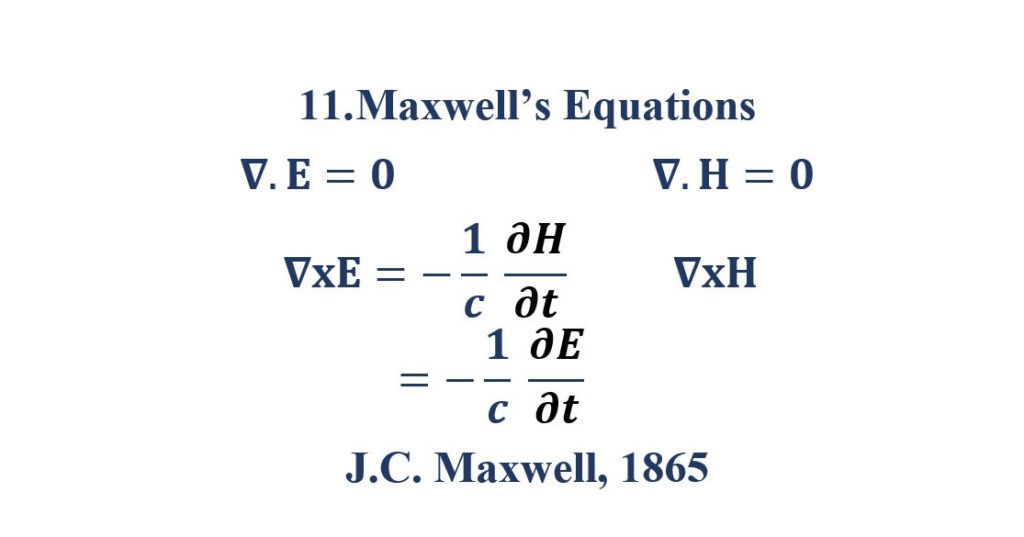
Maxwell’s equations often involve calculus, there are simplified versions of the equations. These versions only work in certain circumstances, but can be useful and save a lot of trouble.
12. Second Law of Thermodynamics
The second law of thermodynamics states that the total entropy of an isolated system can never decrease over time, and is constant if and only if all processes are reversible. Isolated systems spontaneously evolve towards thermodynamic equilibrium, the state with maximum entropy.
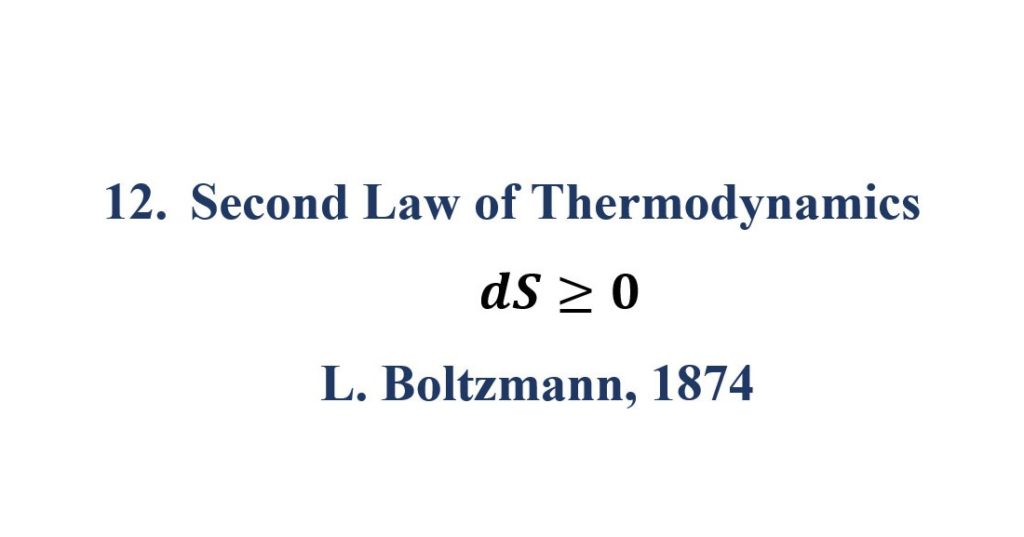
13. Relativity
The increased relativistic mass (m) of body times the speed of light squared (c2) is equal to the kinetic energy (E) of that body. E = mc2 Proof of Albert Einstein’s special-relativity equation E = mc2.
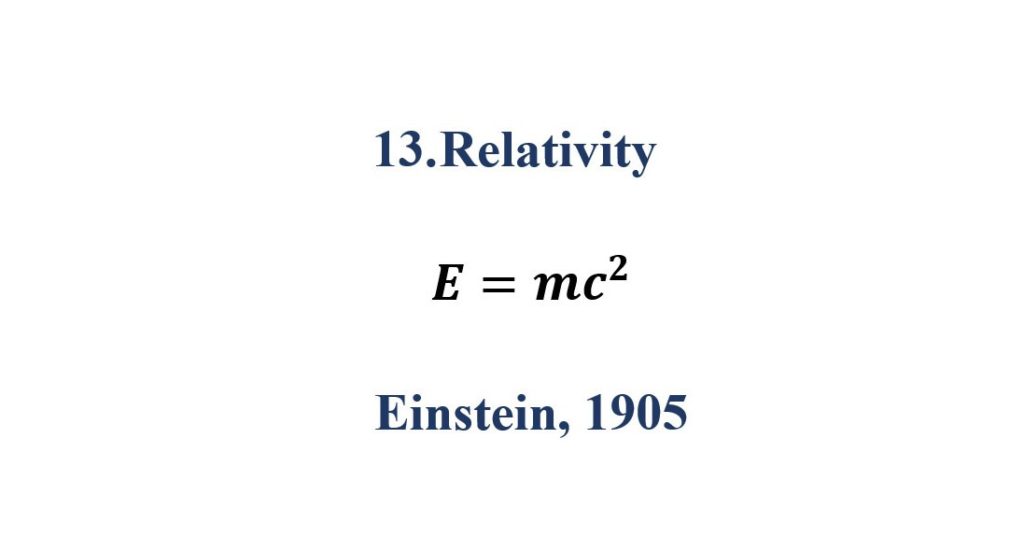
Applications of Relativity Equations
- The production of nuclear power from Uranium and plutonium relies on the principles of radioactivity, derived by E=mc^2
- The Atom Bomb based on both Fusion and Fission reaction has its destructive power as a direct result of the equation.
- The radioactivity of various elements that result in the production of x rays, gamma rays and what not are attributed to this equation.
14. Schrodinger’s Equation
Schrödinger equation is a mathematical equation that describes the changes over time of a physical system in which quantum effects, such as wave particle duality, are significant.
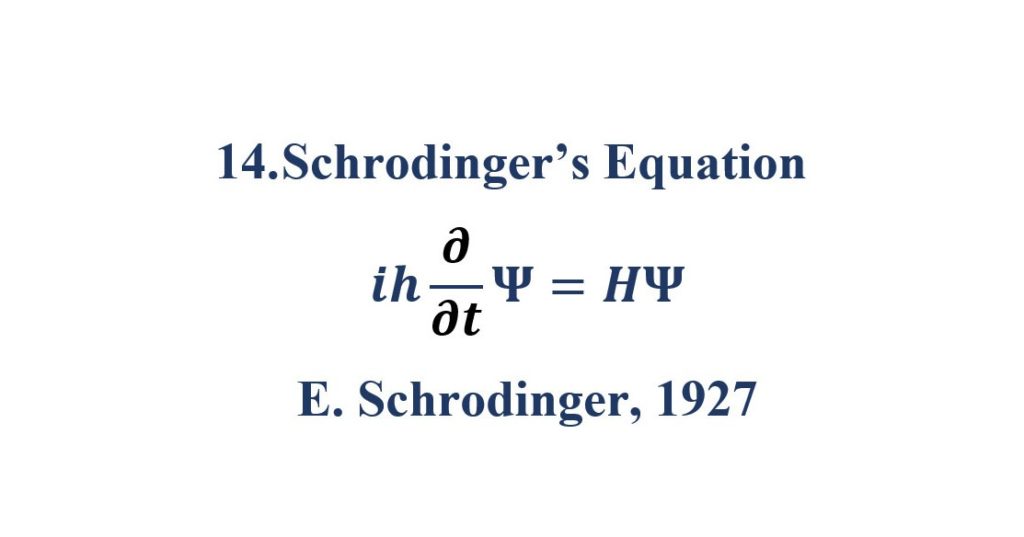
The Schrodinger equation is used to find the allowed energy levels of quantum mechanical systems (such as atoms, or transistors). The associated wavefunction gives the probability of finding the particle at a certain position. The solution to this equation is a wave that describes the quantum aspects of a system.
15. Information Theory
Information entropy (Entropy) is the average rate at which information is produced by a stochastic source of data. The measure of information entropy associated with each possible data value is the negative logarithm of the probability mass function
Applications of Information Theory
- Lossless data compression (e.g. ZIP files).
- Lossy data compression (e.g. MP3s and JPEGs).
- Channel coding (e.g. for digital subscriber line (DSL)).
- An invention of the Compact Disc(CD).
- The feasibility of mobile phones.
- The development of the Internet, numerous other fields.
16. Chaos Theory
The Chaos theory is a study in mathematics to understand the dynamic behavior of nature. The butterfly effect is the best example of chaos theory, small wings flapping in one state can cause big effects at a later stage. Chaos Theory deals with nonlinear things that are effectively impossible to predict or control. it also called the deterministic behavior of the system. Newtonian laws are completely deterministic one.
Principles of Chaos
- The Butterfly Effect: “Small changes in the initial conditions lead to drastic changes in the results”
- Fractals: “Fractal is a pattern. They are complex and created by simple repeating process”
- Unpredictability: “Difficult to predict the ultimate effect of a complex system”
- Feedback: “When feedback is given to the systems, it will get disordered”
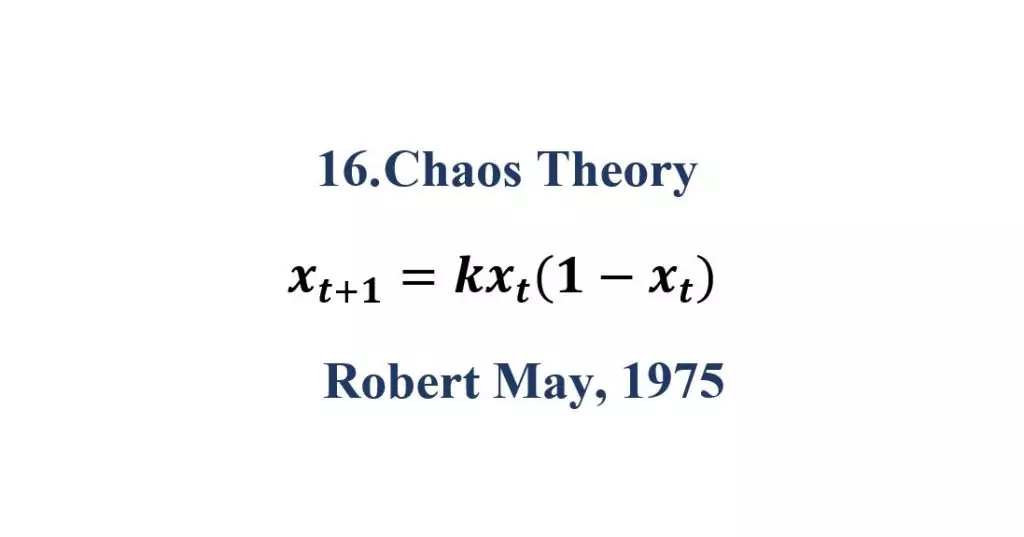
Example fields influenced by Chaos theory
- Game theory
- Machine Learning
- Predictive analytics
- Business Intelligence
- Deep Learning
- Internet of Things
- Bigdata Analytics
- Fuzzy logic and cognitive thinking
17. Black – Scholes Equation
Black–Scholes–Merton model is a mathematical model for the dynamics of a financial market containing derivative
investment instruments.
Applications of Black – Scholes Equation:
- Risk-Neutral valuation
- Market research
- Financial
- Investment
You May Also Love to Read
References – 17 Equations That Changed The World
Real-Life Uses of the Pythagorean Theorem
How is Calculus Used in Everyday Life?
Follow iLovePhD on Pinterest
![Pinterest](https://pinterest.com/pin/create/button/?url=https://www.ilovephd.com/17-equations-that-changed-the-world/&media=https://www.ilovephd.com/wp-content/uploads/2020/05/17-equations-that-changed-the-world-pdf.png&description=In 2013, famous author Ian Stewart published a book "17 Equations That Changed The World". In this article, ilovephd summarise these 17 Equations and its applications.){kind=link}
[…] equation solver is a web application that can solve math equations such as Arithmetic, Algebra, Geometry, Statistics, Differential Equations, Calculus, Discrete […]
[…] 17 Equations That Changed The World […]